Faster than the sound? Our velocity due to Earth's rotation.

We all have heard about relative motion and about relative velocity. "The continuous change of position of a body with respect to a second body or to a reference point that is fixed". 

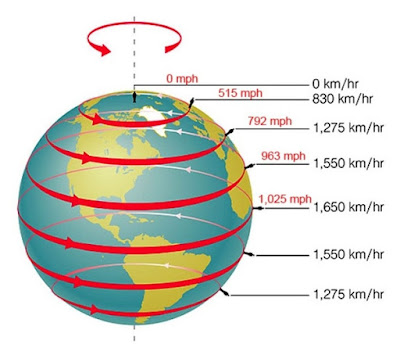
As the Earth is always moving, we can say that we are always at relative move with respect to a reference fixed point. This post presents a simple estimation of the relative velocity of a person located at the Earth's surface with respect to the rotation axis of the Earth. 

We need two data in order to get the relative velocity due to Earth's rotation: Distance to the rotation axis (radius) and the rotation period.

Distance to the rotation axis

The Earth is not a sphere, but an ellipsoid, flattened slightly at the poles and bulging somewhat at the Equator. The ellipsoid is used as a surface of reference for the mathematical reduction of geodetic and cartographic data.

The standard geodetic system to describe the Earth is the World Geodetic System 1984 (WGS84). It describes the Earth as an ellipsoid with a semi major axis of 6,378,137 m and a semi menor axis of 6,356,752 m.

Thus, the rotation radius for someone at the Equator is (Re) 6,378,137 m.

In order to get the rotation at a different latitude, we simply multiply the distance from the center of the Earth to that point by the cosine of the latitude. Since the radius is varying, for simplicity we will just assume the media of semi major and the semi minor axis.

Average radius (Ra) = (6,378,137 + 6,356,752) * 0.5 = 6,371,944.5 m

Rotation period

For the example we will consider the Earth's sidereal day, i.e., he length of time which passes between a given "fixed" star in the sky crossing a given projected meridian. Although some research suggests that the Earth is slowing down, in the current example sidereal day is assumed as constant equal to 23 hours 56 minutes 4.1 seconds. This is equivalent to 86,164.1 seconds.

Calculate

A spot on the Earth's equator traces out a full circle every sidereal day. The circumference of this circle (C) can easily be calculated by using the basic equation:

C = 2 π Re

C = 40,075,110 m

The spot on the Earth's equator travels this full circumference every sidereal day (Sd). Therefore the speed of a person standing on the equator (Ve) can be calculated by using the following equation:

Ve = Ce / Sd

Sd = 23 hours 56 minutes 4.091 seconds

Ve = 465.1 m/s

Which is faster the the speed of sound (340.29 m/s).

Now let's consider someone at a longitude 66 degree North, which is the farthest North extreme of Iceland. The circumference circle is:

C = 2 π Ra cos (66) = 2,591,703 m

Then, the speed of someone at 66 degrees north is 189.17 m/s, which is lower than the speed of sound.

The latitude that travels at speed of sound is 42.97 degrees. This is the latitude of Milwaukee in the Norther hemisphere and Tasmania in the Southern hemisphere.

Anyway, all of them are very high velocities. The reason why we cannot feel such velocities is because the Earth's rotational speed is quite constant and therefore has a negligible acceleration and the Earth's gravity keeps us well grounded.

References and Additional Reading

Defense Mapping Agency Technical Manual 8385.1

From Sundials to Atomic Clocks. Understanding Time and Frequency